1.1 통계 학습의 개요
통계 학습(statistical learning)은 데이터를 이해하고 분석하기 위한 다양한 도구들의 모음이다. 이러한 도구들은 지도(supervised) 학습 또는 비지도(unsupervised) 학습으로 분류될 수 있다.
지도적 통계 학습은 하나 이상의 입력(input) 변수를 기반으로 출력(output) 변수를 예측하거나 추정하는 통계적 모델을 만드는 것과 관련된다. 이는 비즈니스, 의학, 천체물리학, 공공 정책과 같은 다양한 분야에서 사용된다.
비지도 통계 학습은 출력 변수 없이 입력 변수만을 가지고, 자료의 상관관계(두 변수 간의 관계)와 구조를 파악하는 데 사용된다.
1.1.1 Wage자료
이 자료는 미국 대서양 지역에 거주하는 한 그룹의 남성들을 대상으로, 임금(wage)과 관련된 다양한 요소들을 분석하는 데 사용된다. 특히 고용인의 나이(age), 교육 수준(education), 그리고 임금을 받은 연도(year)와의 관련성을 이해하고자 한다.
왼쪽 패널의 그림은 개개인의 임금(wage)을 나이(age)에 따라 나타낸 것이다. 임금(wage)은 나이가 증가함에 따라 상승하지만, 대략 60세 이후에는 다시 감소하는 경향이 있음을 알 수 있다. 그림에서 파란색 선은 주어진 나이에 대한 평균 임금의 추정값을 나타내며, 추세(trend)를 명확하게 보여준다. 고용인의 나이가 주어지면, 이 곡선을 사용해 그의 임금을 예측할 수 있다. 그러나 이 평균값에는 상당한 변동성이 있어, 나이만으로는 남성의 임금을 정확하게 예측하기 어렵다.
연도(year)를 보면, 2003년과 2009년 사이의 임금 증가는 대략 $10,000으로 거의 선형적이며, 데이터의 변동성에 비해 매우 작은 변화이다. 또한, 임금은 교육 수준이 높을수록 더 높게 나타난다. 주어진 남성의 임금(wage)에 대한 가장 정확한 예측은 그의 나이(age), 교육 수준(education), 그리고 연도(year)를 함께 고려함으로써 얻을 수 있을 것이다.

1.1.2 주식시장 자료
Wage 자료는 연속적(continuous) 또는 양적(quantitative) 출력값을 예측하는 것과 관련된다. 이는 흔히 회귀(regression) 문제라고 한다.
- 연속적 출력값: 연속적으로 값을 가지는 변수로, 키, 체중 등이 있다.
- 양적 출력값: 수입, 주가, 판매량 등이 이에 해당한다.
아래 그림은 과거 5일(5년) 동안의 주가지수 변동을 이용해 주어진 날짜에 주가지수가 상승할지 또는 하락할지를 예측하는 것이다. 여기에서 통계 학습 문제는 수치를 예측하는 것과 관련되지 않는다. 대신, 주어진 날짜에 주식시장이 상승(Up) 또는 하락(Down) 국면에 있을지를 예측하는 것이 관련되며, 이것은 분류(classification) 문제로 알려져 있다.
왼쪽 패널은 백분율로 나타낸 전날의 주가지수 변동을 두 개의 박스 도표로 나타낸 것이다. 하나는 그다음 날 주식시장이 상승한 647일에 대한 도표이고, 다른 하나는 그다음 날 주식시장이 하락한 602일에 대한 도표이다.
두 도표는 거의 동일하게 보이며, 이는 어제의 S&P 지수 움직임을 이용해 오늘의 수익률을 예측할 수 있는 간단한 방법이 없다는 것을 시사한다.

1.1.3 유전자 발현 자료
앞의 두 자료(지도 학습)는 입력 변수와 출력 변수를 모두 가지고 있는 경우를 다룬다. 하지만 비지도 학습에서는 입력 변수들만 관측할 수 있고, 그에 대응하는 출력 변수는 없는 경우도 있다.
예를 들어, 마케팅에서는 다수의 고객에 대한 인구 통계적 정보를 가지고 있을 수 있으며, 우리는 관찰된 특징에 따라 고객들을 그룹화하여 어떤 유형의 고객들이 서로 유사한지를 이해하려고 할 수 있다. 이것은 클러스터링(clustering) 문제로 알려져 있으며, 여기서는 출력 변수를 예측하지 않는다.
NC160 자료는 64개의 암 세포주(cell lines) 각각에 대한 6,830개의 유전자 발현 측정치로 구성된다.
- 64개의 암 세포주: 64개의 서로 다른 유형의 암 세포주.
- 6,830개의 유전자 발현 측정치: 각 암 세포주마다 6,830개의 유전자 발현 데이터가 존재한다.
여기서는 특정 출력 변수를 예측하는 대신, 유전자 발현 측정치를 기반으로 세포주들 사이에 그룹 또는 클러스터가 있는지 파악하는 데 관심이 있다.
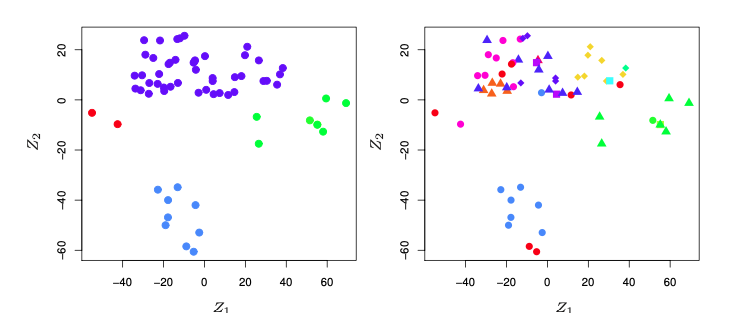
$Z_1$과 $Z_2$는 데이터의 처음 두 개의 주성분(principal components)으로, 각 세포주의 6,830개의 발현 관측치를 두 개의 수 또는 차원으로 요약한 것이다.
- 주성분: 고차원 데이터를 저차원으로 축소하면서, 가능한 한 많은 정보를 유지하려고 한다. (6,830개의 고차원 데이터를 2개의 저차원 데이터로 축소)
그림의 왼쪽 패널은 서로 다른 색깔로 표시된 적어도 4개의 세포주 그룹이 존재함을 시사한다. 오른쪽 패널은 왼쪽 패널과 동일한 그림이지만, 14개의 서로 다른 암 유형이 다른 색깔의 기호로 표시되어 있다. 동일한 암 유형을 가진 세포주들은 이 2차원 표현에서 서로 가깝게 위치하는 경향이 명백하게 나타난다.
1.2 통계학습의 간단한 역사
19세기 초반, 르장드르(Legendre)와 가우스(Gauss)는 최소 제곱법에 대한 논문을 발표하였으며, 이 논문에서 지금은 선형 회귀(linear regression)로 알려진 방법을 제시하였다. 선형 회귀는 개인의 급여와 같은 양적 값을 예측하는 데 사용된다.
환자가 생존하거나 사망할지, 또는 주식시장이 상승하거나 하락할지와 같은 질적 값을 예측하기 위해, 피셔(Fisher)는 1936년에 선형 판별 분석(linear discriminant analysis)을 제안하였다. 1940년대에는 여러 저자들이 대안적인 방법으로 로지스틱 회귀(logistic regression)를 제안하였다.
1970년대 초, 넬더(Nelder)와 웨더번(Wedderburn)은 통계 학습 방법을 총망라한 일반화된 선형 모델(generalized linear model)이라는 용어를 만들어냈으며, 선형 회귀와 로지스틱 회귀는 그 특수한 경우로 여기에 포함된다.
1980년대 중반, 브라이먼(Breiman), 프리드먼(Friedman), 올쉔(Olshen), 스톤(Stone)은 분류 및 회귀 나무(classification and regression tree)를 도입하였으며, 모델 선택을 위한 교차 검증을 포함하여 처음으로 실질적인 구현과 그 유용성을 보여주었다.
해스티(Hastie)와 티브시라니(Tibshirani)는 1986년에 일반화된 선형 모델의 비선형적 확장에 대한 일반화 가법 모델(generalized additive model)을 제안하였으며, 이를 실용적인 소프트웨어로 구현하였다.
1.3 표기법과 간단한 행렬 대수
데이터 표본에서 데이터 포인트의 수 또는 관측치의 수는 $n$으로 나타낸다. 예측에 사용할 수 있는 변수의 수는 $p$로 나타낸다. 예를 들어, Wage 자료는 3,000명의 사람에 대해 12개의 변수로 구성되며, 따라서 $n = 3,000$개의 관측치와 $p = 12$개의 변수(year, age, wage 등)를 가진다.
일반적으로, $i$번째 관측치에 대한 $j$번째 변수의 값은 $x_{ij}$로 나타내며, 여기서 $i$(관측치)는 $1, 2, \dots, n$이고, $j$(변수)는 $1, 2, \dots, p$이다. $X$는 n(행) x p(열) 행렬을 나타낸다.
$x_i = \begin{pmatrix} x_{i1} \\ x_{i2} \\ \vdots \\ x_{ip} \end{pmatrix}$
여기서 $x_i$는 길이가 $p$인 벡터로, $i$번째 관측치에 대한 $p$개의 변수 값을 포함한다. 예를 들어, Wage 자료의 경우, $x_i$는 길이가 12인 벡터이며, $i$번째 사람에 대한 year, age, wage, 그리고 다른 변수들의 값을 포함한다.
$x_j = \begin{pmatrix} x_{1j} \\ x_{2j} \\ \vdots \\ x_{nj} \end{pmatrix}$
예를 들어, Wage 자료의 경우, $X_1$은 year에 대한 $n = 3,000$개의 값을 포함한다. 이 표기법을 사용하면, 행렬 $X$는 다음과 같이 표기할 수 있다. $X = (X_1 \quad X_2 \quad \dots \quad X_p)$
여기서 $T$는 행렬 또는 벡터의 전치(transpose)를 나타낸다.
$X = \begin{pmatrix}x_1^T \\x_2^T \\\vdots \\x_n^T\end{pmatrix}$
반면에, $x^T_i = (x_{i1} \quad x_{i2}\quad \dots \quad x_{ip})$이다.
$X^T = \begin{pmatrix}x_{11} & x_{21} & \cdots & x_{n1} \\x_{12} & x_{22} & \cdots & x_{n2} \\\vdots & \vdots & \ddots & \vdots \\x_{1p} & x_{2p} & \cdots & x_{np}\end{pmatrix}$
관측된 데이터는 ${(x_1, y_1),(x_2, y_2), \dots, (x_n, y_n)}$로 구성되며, 여기서 $x_i$는 길이가 $p$인 벡터이다. 만약 $p=1$이면, $x_i$는 단순히 스칼라(단일 숫자 값)이다. 예를 들어, $x_i$는 한 학생의 여러 과목 성적(수학, 영어, 과학 등)을 나타낼 수 있다. $y_i$는 해당 학생의 최종 성적일 수 있다. (예: 합격 또는 불합격)
객체가 스칼라인 경우 $a ∈ R$로 나타내고, 길이가 $k$인 벡터는 $a ∈ R^k$로 표현한다. 객체가 $r$ x $s$ 행렬인 경우에는 $A ∈ R^{r *s}$로 나타낸다.
두 행렬의 곱셈에 대한 개념을 이해하는 것이 중요하다. $A ∈ R^{r*d}$와 $B ∈ R^{d*s}$가 있다고 가정하자. 이때 $A$와 $B$의 곱은 $AB$로 나타낸다. $AB$의 $(i, j)$번째 원소는 $A$의 $i$번째 행의 각 원소와 $B$의 $j$번째 열의 대응하는 원소를 곱한 후, 그 합으로 계산된다. 즉, $(AB)_{ij} = \sum_{k=1}^{d} a_{ik} b_{kj}$이다.
위 식은 $A$의 열의 개수와 $B$의 행의 개수가 동일할 때(즉, $d$일 때)만 계산이 가능하다.
$\begin{equation*}AB = \begin{pmatrix}1 & 2 \\3 & 4\end{pmatrix}\begin{pmatrix}5 & 6 \\7 & 8\end{pmatrix}= \begin{pmatrix}1 \times 5 + 2 \times 7 & 1 \times 6 + 2 \times 8 \\3 \times 5 + 4 \times 7 & 3 \times 6 + 4 \times 8\end{pmatrix}= \begin{pmatrix}19 & 22 \\43 & 50\end{pmatrix}\end{equation*}$
'AI > ISLR' 카테고리의 다른 글
| Chapter02. 통계학습(Statistical Learning) - 이론 (15) | 2024.09.07 |
|---|---|
| Chapter 05. 재표본추출 방법(Resampling Methods) - 이론 (9) | 2024.09.03 |
| Chapter 04. 분류(Classification) - 실습 (9) | 2024.09.02 |
| Chapter 04. 분류(Classification) - 이론 2 (8) | 2024.08.28 |
| Chapter 04. 분류(Classification) - 이론 1 (5) | 2024.08.21 |


댓글